Introduction
SNOVA is a digital signature algorithm that was submitted to the NIST Post-Quantum Cryptography Project in May 2023, its full name is βSimple Noncommutative-ring based UOV with key-randomness Alignmentβ, SNOVA is a simplified version of NOVA.
Features
The SNOVA digital signature algorithm is a variant of the UOV algorithm, retaining the UOV's
characteristic of short signatures while offering a shorter public key length compared to the
traditional UOV algorithm, thereby providing advantages in both security and efficiency aspects of
digital signatures.
Furthermore, the SNOVA algorithm provides three different parameter options for each security level,
including various combinations of public key and signature lengths. This feature brings greater
flexibility and adaptability to the application side, enabling SNOVA to be well-suited for diverse
scenarios, whether it be resource-constrained devices or applications requiring high-security
protection, as it allows for the selection of parameter configurations that best suit the specific
use case.
Parameters
| SL | (v, o, q, l) | public key size | sign size | private key size (esk) | private key size (ssk) |
|---|---|---|---|---|---|
| I | (37, 17, 16, 2) | 9826(+16) | 108(+16) | 60008(+48) | 48 |
| (25, 8, 16, 3) | 2304(+16) | 148.5(+16) | 37962(+48) | ||
| (24, 5, 16, 4) | 1000(+16) | 232(+16) | 34112(+48) | ||
| III | (56, 25, 16, 2) | 31250(+16) | 162(+16) | 202132(+48) | |
| (49, 11, 16, 3) | 5989.5(+16) | 270(+16) | 174798(+48) | ||
| (37, 8, 16, 4) | 4096(+16) | 360(+16) | 128384(+48) | ||
| V | (75, 33, 16, 2) | 71874(+16) | 216(+16) | 515360(+48) | |
| (66, 15, 16, 3) | 15187.5(+16) | 364.5(+16) | 432297(+48) | ||
| (60, 10, 16, 4) | 8000(+16) | 560(+16) | 389312(+48) |
Table of key-sizes and lengths of the signature of SNOVA parameter settings. (bytes)
Security & Sizes
Direct attack. An attacker need to regard a SNOVA public map as an UOV public map over π½ and then forge a signature. This gives an MQ(πΒ²π, πΒ²π, π) system.
Collision attack. To forge a fake signature, an attacker checks π intended signatures and π hash values whether there exists a collision or not.
KS/Reconciliation/Intersection attacks. From the viewpoint of key recovery, an attacker can regard a (π£, π, π, π) SNOVA scheme over ring as an (ππ£, ππ, π) UOV scheme with πΒ²π equations over π½.
| Table of security (in log #gates) and sizes | ||||||||
| SL | (v, o, l) | Dir | KS | Rec | Int | Col | pk(Bytes) | sig(Bytes) |
| I | (37, 17, 2) | 165/123 | 165/85 | 203 | 153 | 151 | 9842 | 124 |
| (25, 8, 3) | 171/126 | 209/107 | 200 | 221 | 159 | 2320 | 164.5 | |
| (24, 5, 4) | 184/134 | 309/157 | 269 | 353 | 175 | 1016 | 248 | |
| III | (56, 25, 2) | 234/173 | 253/129 | 297 | 221 | 215 | 31266 | 178 |
| (49, 11, 3) | 226/162 | 461/233 | 438 | 529 | 213 | 6005.5 | 286 | |
| (37, 8, 4) | 287/214 | 469/237 | 387 | 506 | 271 | 4112 | 376 | |
| V | (75, 33, 2) | 302/222 | 341/173 | 389 | 288 | 279 | 71890 | 232 |
| (66, 15, 3) | 302/220 | 617/311 | 574 | 690 | 285 | 15203.5 | 380.5 | |
| (60, 10, 4) | 350/255 | 805/405 | 695 | 922 | 335 | 8016 | 576 | |
Comparison
A comparison of the key and signature sizes of SNOVA, and the key and signature sizes of the NISTPQC finalists (SPHINCS+, DILITHIUM and Falcon), Pre-Quantum (RSA and EdDSA) and compressed UOV.
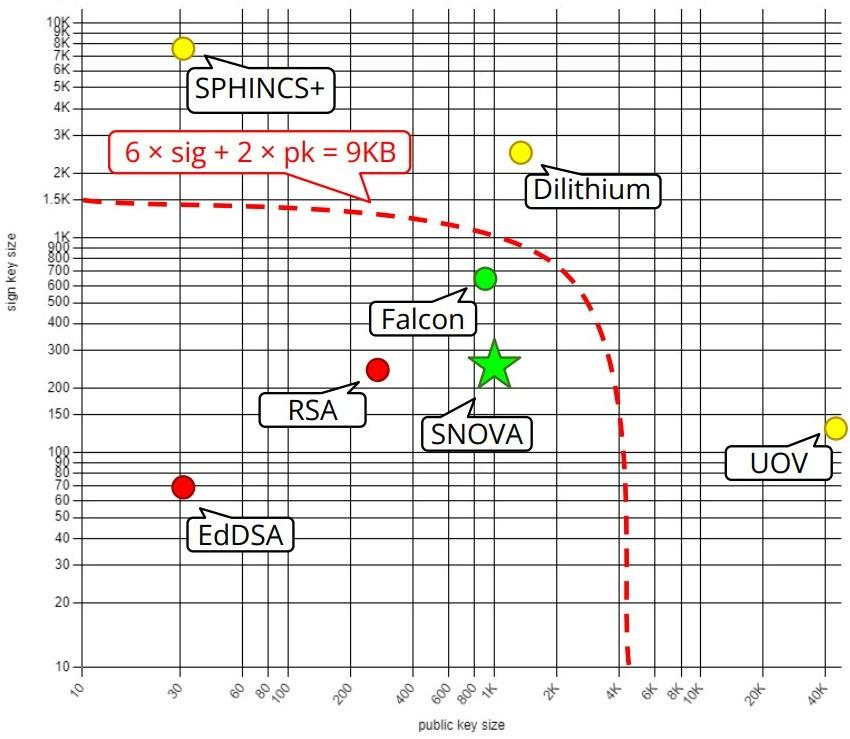
Making Internet post-quantum. For easily upgrading existing protocols (e.g. TLS) to become quantum-resistant, the article of CloudFlare gives the condition: 6 x signature + 2 x pk β€ 9KB.
Performance
Here are the optimization results for SNOVA on the (Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz, Skylake) platform using AVX2-related instructions. We have achieved approximately a 50-fold increase in efficiency compared to the previous version.
| SL | (v,o,l) | Gen cycles | Gen/s | Sign cycles | Sign/s | Verify cycles | Verify/s |
| I | (24,5,4) | 904,287 | 3,760 | 713,054 | 4,768 | 168,300 | 20,202 |
| III | (37,8,4) | 5,497,621 | 618 | 2,206,664 | 1,541 | 577,521 | 5,887 |
| V | (60,10,4) | 18,096,522 | 188 | 5,099,659 | 667 | 1,641,880 | 2,071 |
These achievements indicate significant prospects for the application of SNOVA in most scenarios.
Resources
NIST Submission Package for Round 1 Additional Signatures
It is the zip archive that we submitted to the Round 1 Additional Signatures of the NIST PQC
project. It contains the specification of SNOVA, the reference implementation.
Download
NIST submission package for Round 1 Additional Signatures (zip)
NIST Submission Document for Round 1 Additional Signatures
It is the pdf archive that we submitted to the Round 1 Additional Signatures of the NIST PQC
project. It contains the specification of SNOVA, the Document.
Download
NIST submission document for Round 1 Additional Signatures (pdf)
Cryptology ePrint Archive: A Simple Noncommutative UOV Scheme
In this paper, we propose a simple noncommutative-ring based UOV signature scheme with
key-randomness alignment: Simple NOVA, which can be viewed as a simplified version of NOVA
Updated on 2024-02-08